Given an unlabeled dataset, we’d like to group the data into coherent clusters. These types of problems can be solved using an unsupervised learning algorithm, such as the K-means algorithm.
The code I’m going to discuss is written using the Octave programming language. Octave is a free (as in freedom) software developed and published by the Free Software Foundation.
The code is publicly available from my Github repository.
Let’s get started. For the impatient ones, here’s the entire code. To understand what’s going on, read the discussion that follows.
%% ========================================================================
%% The Kmean algorithm. Tested with Octave.
%%
%% Inputs:
%% K - Number of clusters.
%% X - Training set, {x(1); x(2); x(3); ...; x(m)}; where each
%% x(i) is a point in space. X is a m*2 matrix.
%% MAXITR - Maximum number of iterations.
%%
%% Output:
%% idx - Cluster indices, This is a numeric column vector.
%% idx has as many rows as X, and each row indicates the
%% cluster assignment of the corresponding observation.
%% centers - Column vector containing cluster centers. K*2 matrix.
%% ========================================================================
function [idx centers] = Kmean(K, X, MAXITR)
m = size(X, 1); % Number of sample points
if(K > m) % Breaking condition
fprintf('>>> Error! K must be less than the number of sample points.\n\n'); fflush(stdout);
else
% Randomly initialize K cluster centers
centers = zeros(K, 2);
perm = randperm(m);
perm = perm(1:K);
centers = double(X(perm, :));
% initializing some more variables
d = zeros(K, 1);
idx = zeros(m, 1);
% K-means clustering
fprintf('Begin K-mean clustering..'); fflush(stdout);
for n = 1:MAXITR
% Step 1 - Cluster assignments
for i = 1:m
x = [X(i, :)];
for k = 1:K
c = [centers(k,:)];
d(k) = ((x(1) - c(1))^2) + ((x(2) - c(2))^2);
end
[minval idx(i)] = min(d);
end
% Step 2 - Move cluster centers
for k = 1:K
cluster_points = [];
for i = 1:m
if(idx(i) == k)
cluster_points = [cluster_points; X(i, :)];
end
end
if (size(cluster_points, 1) > 1)
centers(k, :) = mean(cluster_points);
else
centers(k, :) = cluster_points(:);
end
end
end
fprintf('Done.\n'); fflush(stdout);
end
end
Here’s a demo showing how you can use the above function:
% Testing Kmean algorithm. Tested with Octave.
clear; clc;
K = 3;
% X = 100.*rand(90, 2);
X = [randn(100,2)*0.75+ones(100,2);
randn(100,2)*0.5-ones(100,2)];
[idx centers] = Kmean(K, X, 10);
figure;
hold on
title 'Kmean Clustering Example';
plot(X(idx==1, 1), X(idx==1, 2), 'r.', 'MarkerSize', 6);
plot(X(idx==2, 1), X(idx==2, 2), 'g.', 'MarkerSize', 6);
plot(X(idx==3, 1), X(idx==3, 2), 'b.', 'MarkerSize', 6);
plot(centers(:, 1), centers(:, 2), 'kx', 'MarkerSize', 12, 'LineWidth', 3);
legend('Cluster 1', 'Cluster 2', 'Cluster 3', 'Centroids', 'Location', 'NorthWest');
hold off
Once you run the above code, you shall see an output similar to the following figure:
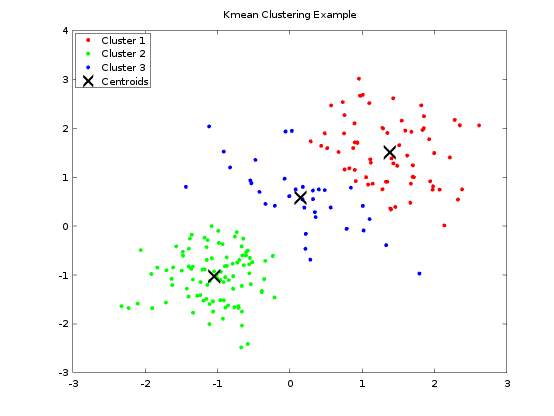
The figure shows several points in space grouped into three clusters.
The explanation is rather simple. Let us assume, we have m data points and want to group the data in K (K < m) coherent clusters. At first, we randomly initialize K data points as cluster centers. K-means is an iterative algorithm. The algorithm works in two major steps. The two steps are,
- Cluster assignment and,
- Move centroid.
The first of the two steps in the inner loop of Kmeans is the cluster assignment step. In this step, each data point is assigned to one of the K clusters. What it essentially means is that we take each example or each data point and depending on their distance from each of the cluster centers, we assign the data points to one of the K clusters.
The second step (also in the inner loop) is the move centroid step. What we are going to do is we are going to move each of the cluster centers to a new location. The new location for the first cluster center is determined by taking the average (or mean) of all the data points in the first cluster. And we do the same for all the cluster centers.